Numpyでグラフ
今期からPCでのレポート作成が可能になった。
図などは手書きで後から書き込んでいるので周りから笑われがちだが、
グラフは我ながら少なくとも手書きとグラフ用紙ではできないものを(短時間で(ささっと(手抜き)))作っている
と思う。numpyでグラフを書く人が増えることを祈って今期の実験で使った
ゴミスクリプトをまとめてみた。だが悲しいかな、次の実験は有機である。したがって
筆者の自己満足である。
なお、コマンドラインにそのまま貼り付けてもうまく動かない可能性があるので、動かしてみたいと思う ならエディタで整形して欲しい。 実行にはnumpy、matplotlib、scipyなどが必要と思う。ここのスクリプトが正しく動く、あるいは 正しい結果を示すことは一切保証できないことに注意。
◇Mass
Massの実験で作ったものが一番行数が長い。 3Dと2Dで表示するようにした。(が、計算には自信なし)
2Dバージョン
実験で使われるマシンの値で計算。Massの2つの加速領域のうち、どちらか一方の電圧を固定して 飛行時間のグラフを描く。
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.ticker import ScalarFormatter
Na = 6.0221408*10**23
m = 28 # N2分子
s0 = 1.10 / 100 # m単位
d0 = 2.20 /100
d = 2.32 / 100
dx = 0.4 /100
D = 13.495 /100
q = 1 # 1荷のカチオン
e0 = 1.6021766*10**(-19)
def v1 (V1,V2,s0):
return np.sqrt( (2*q*e0* (V1*(s0/d0) ) )/(m/Na) *1000)
def v2 (V1,V2,s0):
return np.sqrt( (2*q*e0*(V1*(s0/d0)+V2))/(m/Na) *1000)
def t1 (V1,V2,s0):
return 2 * s0 / v1(V1,V2,s0)
def t2 (V1,V2,s0):
return 2 * d / ( v1(V1,V2,s0) + v2(V1,V2,s0) )
def t3 (V1,V2,s0):
return D / v2(V1,V2,s0)
def t_all (V1,V2,s0):
return t1(V1,V2,s0) + t2(V1,V2,s0) + t3 (V1,V2,s0)
# -*- 2D -*-
V1_X = 160 #160V固定
V2_Y = np.arange(200,920 , 0.1)
T1 = t_all(V1_X,V2_Y,s0)
T2= t_all(V1_X,V2_Y,s0+dx)
plt.plot(V2_Y, T1)
plt.plot(V2_Y, T2)
plt.xlabel(u"電圧",fontdict={'family': u'IPAGothic'})
plt.gca().yaxis.set_major_formatter(ScalarFormatter(useMathText=True))
plt.ylabel(u"飛行時間",fontdict={'family': u'IPAGothic'})
plt.gca().ticklabel_format(style="sci", axis="y",scilimits=(0,0),fontdict={'family': u'IPAGothic'})
plt.show()
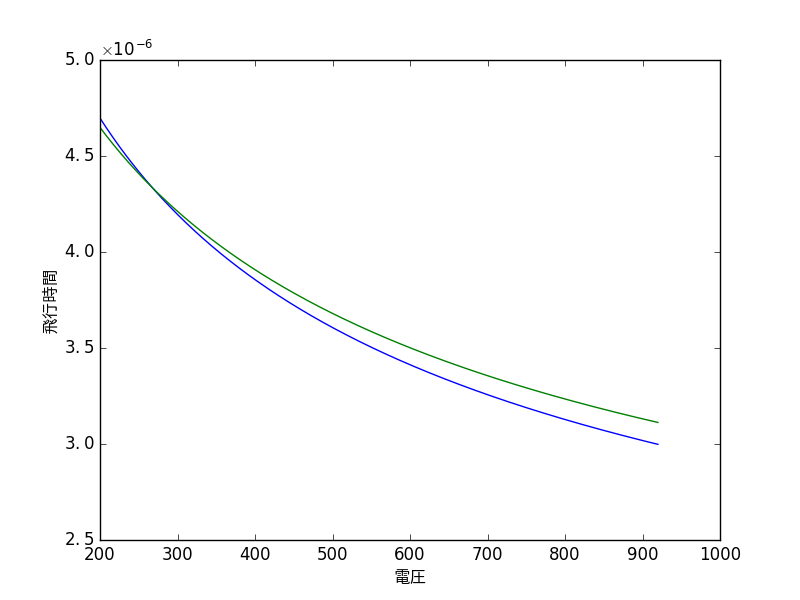
重なる点がある(正常)
3Dバージョン
2つの加速領域の電圧を独立に変えた時、粒子の飛行時間はどうなるかを表すグラフを描く。
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
import numpy as np
import matplotlib.ticker as ptick
from matplotlib.ticker import ScalarFormatter
Na = 6.0221408*10**23
m = 28 # N2分子
s0 = 1.10 / 100 # m単位
d0 = 2.20 /100
d = 2.32 / 100
dx = 0.4 /100
dx2 = 0.5 /100
D = 13.495 /100
q = 1 # 1荷のカチオン
e0 = 1.6021766*10**(-19)
def v1 (V1,V2,s0):
return np.sqrt( (2*q*e0* (V1*(s0/d0) ) )/(m/Na) *1000)
def v2 (V1,V2,s0):
return np.sqrt( (2*q*e0*(V1*(s0/d0)+V2))/(m/Na) *1000)
def t1 (V1,V2,s0):
return 2 * s0 / v1(V1,V2,s0)
def t2 (V1,V2,s0):
return 2 * d / ( v1(V1,V2,s0) + v2(V1,V2,s0) )
def t3 (V1,V2,s0):
return D / v2(V1,V2,s0)
def t_all (V1,V2,s0):
return t1(V1,V2,s0) + t2(V1,V2,s0) + t3 (V1,V2,s0)
# -*- 3D -*-
v1_x = np.arange(0, 100, 5)
v2_y = np.arange(0, 100, 5)
V1_X, V2_Y = np.meshgrid(v1_x, v2_y)
T = t_all(V1_X,V2_Y,s0)
fig = plt.figure()
ax = axes3d.Axes3D(fig)
ax.plot_wireframe(V1_X,V2_Y,T)
ax.set_xlabel(u"1段目電圧/V",fontdict={'family': u'IPAPGothic'})
ax.set_ylabel(u"2段目電圧/V",fontdict={'family': u'IPAPGothic'})
ax.set_zlabel(u"飛行時間/s",fontdict={'family': u'IPAPGothic'})
ax.zaxis.set_major_formatter(ptick.ScalarFormatter(useMathText=True))
ax.ticklabel_format(style='sci',axis='z',scilimits=(0,0))
plt.title(u"各電圧と飛行時間", fontdict={'family': u'IPAPGothic'})
plt.show()
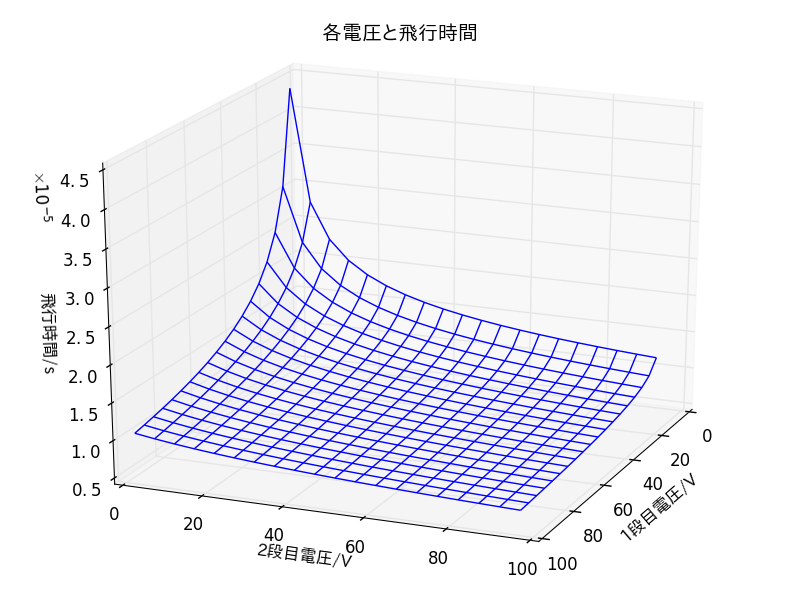
第一加速領域→0で無限になるハズ
リペラーの矩形波
矩形波はどうやってできているか?を考察するためのもの。 ローパスフィルタかけるとどうなるかな、とか考えるときには必要かも。range(1,10)の部分の10を 大きくすると波形が矩形波により近づく。
import matplotlib.pyplot as plt
import numpy as np
def kukei(x_in):
k=0
for n in range(1,10):
k += (1.0 / (2.0*n-1)) * np.sin((2.0*n-1) * 0.1 * np.pi *x_in )
return k
x = np.arange(0, 100, 0.01)
y=kukei(x)
plt.plot(x, y)
plt.show()
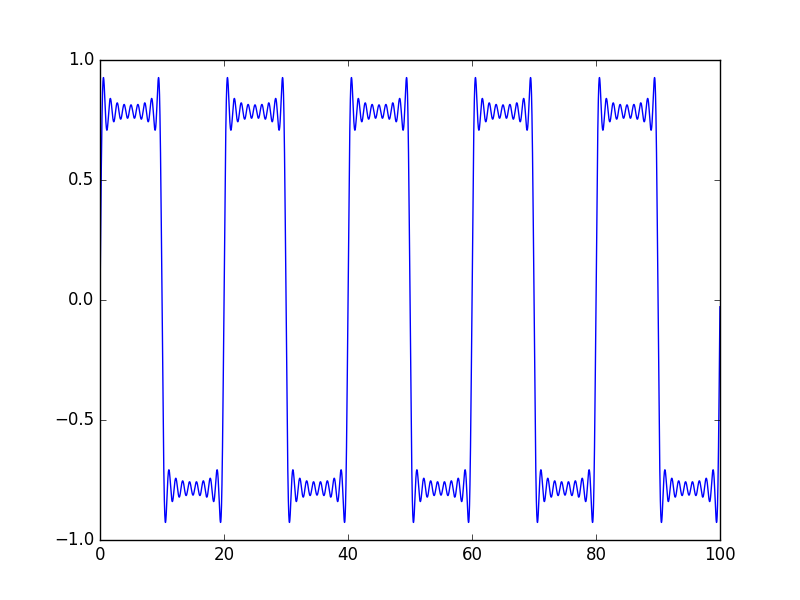
矩形波
◇特別実験(fsレーザー)
正直、結果の解釈に自信がない。
波の重ねあわせ
fsレーザーは多数の波長の波の重ね合わせで鋭いパルスを作るらしい。そのイメージで作った。
import matplotlib.pyplot as plt
import numpy as np
y_all=0
for i in range(1,10):
x = np.arange(-2, 2, 0.01)
y = np.cos(i*x)
y_all= y_all + y
plt.plot(x, y)
plt.plot(x,y_all)
plt.show()
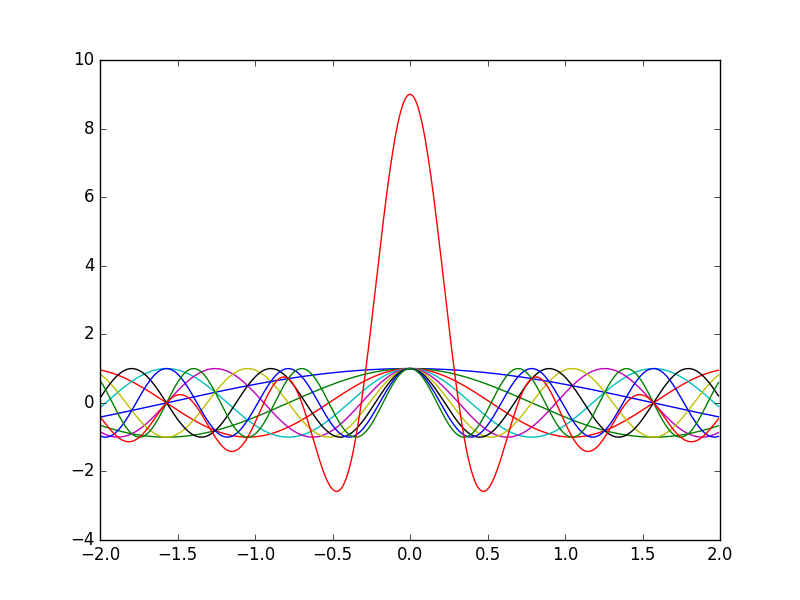
fsパルスのイメージ
高調波発生
第二高調波と元の周波数の波の合成波。(高調波の振幅は小さいだろうから適当に0.25倍しておいた。) これを私は「偏った波っぽいなあ…=>じゃあ結晶中に偏りある」と解釈したのだが、強者が言うにはその解釈は違うらしい。
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(-10, 10, 0.01)
y1 = -np.cos(x)
y2 = np.cos(2*x)*0.25
plt.plot(x, y2,color ="r")
plt.plot(x, y1,color ="b")
plt.plot(x, y1+y2,color ="black")
plt.ylim(-1.5, 1.5)
plt.show()
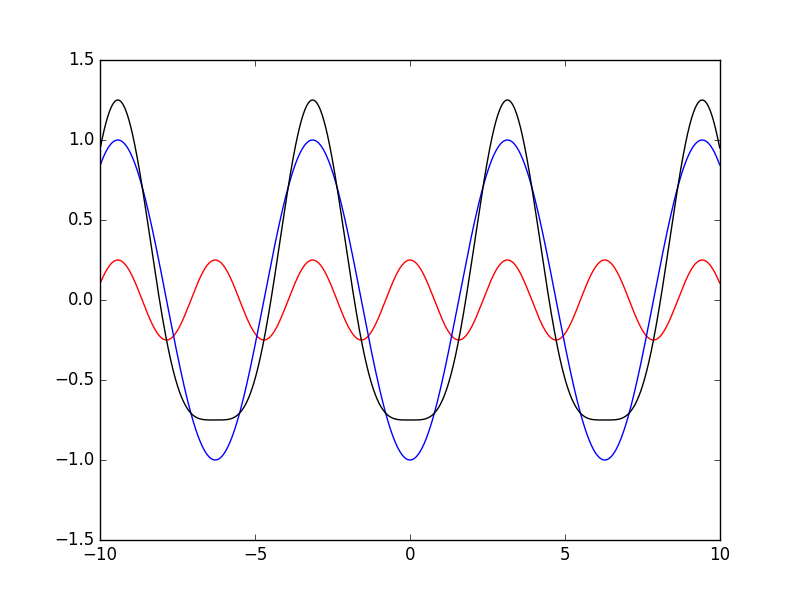
高調波は偏りある結晶構造がいる
◇吸着
csvファイルからデータ読み込んでデータ計算しただけなのに異様に汚い。 関数電卓でもできる(し、関数電卓には物理定数も入っている)のでここにはのせない。
◇割とよく使うTips
凡例/軸タイトルをつける
最低限これがないとグラフ警察に怒られてしまう。
plt.plot(x, y, label = "Data 1") #ラベル付け
plt.legend() #凡例
plt.title(u"グラフタイトル", fontdict={'family': u'IPAPGothic'})
plt.xlabel(u"X軸", fontdict={'family': u'IPAPGothic'})
plt.ylabel(u"Y軸", fontdict={'family': u'IPAPGothic'})
軸の範囲指定
大きめのデータから切り出すときなどに便利。
plt.xlim(小さい方,大きい方) #x軸
plt.ylim(小さい方,大きい方) #y軸
指数表記にする
大きい数/小さい数の時には指数表記にしたい。
# plt を使うとき
from matplotlib.ticker import ScalarFormatter
plt.gca().yaxis.set_major_formatter(ScalarFormatter(useMathText=True)) #yaxis は適宜直す
plt.gca().ticklabel_format(style="sci", axis="y",scilimits=(0,0)) #axis="y" は適宜直す
# ax を使うときはこちらも可
ax.zaxis.set_major_formatter(ptick.ScalarFormatter(useMathText=True))
ax.ticklabel_format(style='sci',axis='z',scilimits=(0,0))
軸の数字を消す
概念図などの時には軸の数字が邪魔な時がある。
plt.tick_params(labelbottom='off') #x軸
plt.tick_params(labelleft='off') #y軸
ファイルからの読み込み
区切り文字や読み飛ばし行数を簡単に設定できるので、多くのファイルから読み込める。
data = np.loadtxt("ファイル名",delimiter=",", skiprows=1) # ,で区切り、一行飛ばす
x=data[:,0] #1列目
y=data[:,1] #2列目
対数グラフ
plt.semilogy() #y軸が対数
関数フィット
ここのページが詳しい。いろいろ載っている。
◇さいごに
macな人から「gnuplotはいいぞ」「grapherはいいぞ」という声が聞こえた。きれいなグラフを書くには確かにそのほうがいい かもしれないが、numpyは使いやすく、拡張性がある。グラフの範囲を変えたくなっても表計算ソフトと違ってセルをいくつも用意し直す必要もない。 再利用性も高い。関数も変数も簡単に定義でき、連携できる。というわけで「numpyはいいぞ」
かもめ - Make / Walk / Others / About